File : 2a.html
Displaying : QA76.G568/1988 Chapter 3

Three

THE THEORY OF ALGORITHMS

We have seen that algorithms. are a fundamental concept of computer science, and we have developed some insight into how to construct them. In this chapter we will step back a pace to see if there are any interesting properties we can discover about algorithms in general. We will investigate the sorts of problem for which algorithms exist, and the sorts of algorithm which are feasible in terms of their usage of physical resources. Finally we will study methods of increasing one's confidence in an algorithm's correctness.

This chapter is essentially a survey of the theory of algorithms. Some of the results presented are deep and perhaps counterintuitive. Such results require careful mathematical proofs which can be found in the technical literature, but which are omitted or only sketched briefly here. Thus the reader is not expected to see why all the results are true, and such understanding is not required in order to follow the thrust of the chapter.

3.1 Computability

Many examples of algorithms have been presented in Chapter 2. We know there exist algorithms for knitting a sweater, building a model plane, baking a cake, making a dress, and playing a Beethoven sonata. Weknow that computers can control traffic signals, production lines and chemical plants. They can book airline flights, control robots and produce payrolls. There are algorithms for making a cup of coffee, finding the largest of a set of numbers, discovering whether or not a number is prime, and printing the greatest common divisor of two numbers. From our schooldays we remember that there exist algorithms for adding, subtracting, multiplying and dividing numbers, and for computing square roots. No doubt there are algorithms for computing logarithms, finding the frequency of words in a given piece oftext, and controlling a nuclear submarine. Is there-any job which a computercannot do - any job for which no algorithm exists?

The surprising answer is Yes. There are many things a computer cannot do. In fact, the number of things which can be computed is infinitesimal compared with the number of things one might like to compute. Computers cannot do most things!

3. 1.1 History of computability

The idea of having an algorithm, or recipe for performing some task, has existed for thousands of years. For many years, people also held the belief that if any problem could be precisely stated, then withenough effort a solution could eventually be found (or else a proof thatno solution exists could eventually be provided). In other words, it wasbelieved that there was no problem which was so intrinsically difficult that,in principle, it could never be solved.

One of the great supporters of this belief was the famous mathematician David Hilbert (1862-1943). He once said

Hilbert's aim was to devise a formal mathematical system in which all problems can be precisely formulated in terms of statementswhich are either true or false. His idea was to find an algorithm which,given any state merit in the formal system, would determine whether or notthat statement was true. If Hilbert had achieved this objective, then anyproblem which was well-defined could have been solved simply by executingthe algorithm. Deciding the truth of a given statement in the formal systemwas called the Entscheidungs problem by Hilbert, who considered it to bea fundamental open problem inmathematics.

Unfortunately for Hilbert's objective, the 1930s brought a wave of research which showed that the Entscheidungs problem is not computable. That is, no algorithm of the type for which Hilbert longed, exists. A cynic might say that mathematicians could heave a sigh of relief, for if such an algorithm did exist, they would all he out of a job just as soon as the algorithm was found. In fact mathematicians were stunned by this remarkable discovery.

The first news of the discovery came in 1931 when KurtG6del published his now famous incompleteness theorem. Among other things,thisshowed that there is no algorithm whose input can be any statement abouttheintegers and whose output tells whether or not the statement is true.Closelyfollowing on G6del's heels, further mathematicians such as AlonsoChurch,Stephen Kleene, Emil Post, Alan Turing and many others, found moreproblemswhich had no algorithmic solution. Perhaps the most remarkable featureofthose early results on problems which cannot be solved by computers isthatthey were obtained in the 1930s, before the earliest computers had beenbuilt.

3.1.2 The Church-Turing thesis

There is one major obstacle in proving that no algorithm for a particular task exists. We must first know exactly what we mean byan algorithm. Each of the mathematicians mentioned in the previous sectionhad to overcome this obstacle, and each overcame it by defining 'algorithm'in a different way. Godel defined an algorithm as a sequence of rules forforming complicated mathematical functions out of simpler mathematical functions. Church used a formalism called the lambda calculus, whilst Turing used ahypothetical machine we call a Turing machine. Turing defined an algorithmas any set of instructions for his simple machine. In Chapter 2 we definedan algorithmas consisting of basic operations on integers and other datastructures, controlled by sequence, selection and iteration.

Now why should anyone pay any attention to results about algorithms defined in such various and obscure ways? The answer is that all the seemingly different and independently contrived definitions turn outto be equivalent. That is, if something can be computed by an algorithm defined in one way, then it can also be computed by an algorithm defined in any of the other ways. As this equivalence was increasingly realized by researchers in the 1930s, the following two statements became widely believed:

1. All reasonable definitions of 'algorithm' which areknown so far are equivalent.

2. Any reasonable definition of 'algorithm' which anyone will ever make will turn out to be equivalent to the definitions we know.

These beliefs have come to be known as the Church-Turing thesis (or sometimes Church's thesis) after two of the earliest workers who realized the fundamental nature of the concept they had defined. To thisday, no evidence has arisen to the contrary, and the Church-Turing thesisis widely believed.

The Church-Turing thesis merely states that we think we have a good definition for what an algorithm is. Everyone has an intuitive feeling for what it means to perform some task in a routine or mechanical manner. People have an intuitive grasp of the concept of devising a set of instructions or steps to perform some task, and then giving the instructions to a person or machine for purely routine execution. Such a set of instructions is what we think of as an algorithm, and the Church-Turing thesis reassures us that the precise definitions of 'algorithm' used in computer science do indeed match these informal ideas that people have. In short, we believethat whenever we write down some set of steps which we feel could be executedin a purely routine manner, then there is a formal algorithm, in the computer science sense of the word, for the same task.

In a modern setting, we can define 'algorithm' as anything which can he executed on a computer. Fortunately, the particular computer chosen is irrelevant to the definition, since any algorithm which can heimplemented on one computer can also he implemented on any other computer.This is true because all computers can simulate each other: that is, givenany two computers, we can write a program for one computer which can understandand execute any program written for the other. Such a program is called aninterpreter (or simulator or universal program).

The equivalence between all modern computers and theirequivalence to Turing machines and to the numerous other means of defining'algorithm' is further evidence for the Church-Turing thesis.

The existence of interpreters, as discussed above, is in itself an interesting and remarkable property of algorithms. Although itis not self-evident, it is nevertheless true that for any programming language there exists an interpreter which, given the description of any program in the language, can simulate that program. Therefore, the interpreter (or universal program) can perform any task which any other program can perform. This remarkable property of algorithms is called universality.

Loosely speaking, universality means that any computeris equivalent to all other computers in the sense that they can all performthe same tasks. Why then, do people choose one computer over another? Thereason is that some computers run faster than others, some are easier toprogram, some already have programs written for them and it may be uneconomicaltorewrite the program for another computer, and some have more memory sothatlarger programs can execute faster on them. Thus although all computerscanperform the same tasks, they do not necessarily consume the same amountofresources while performing a given task. We shall return to this pointinSection 3.2.

3.1.3 The halting problem

At the beginning of this chapter we mentioned that there are many problems which are non-computable. That is, no algorithm existsfor solving such a problem. This is a very strong statement. We are sayingsomething much deeper than that we don't know an algorithm for solving theproblem.We are saying that we will never know such an algorithm - that wenever canknow such an algorithm, because no such algorithm exists.

In this section we will show how to convince oneself that particular problems are non-computable. The reader may Eke to pause at this point to try to visualize any method for proving that no algorithm can possibly exist for solving a particular problem. Certainly, it is not obvious

We have already mentioned one problem which is not computable. That was Hilbert and Godel's problem concerning facts about numbers. Arethere problems of more direct interest to computer science which are notcomputable? The following paragraphs describe an apparently simple computerscience problem and prove that no algorithm can solve it.

A common problem among computer installations the world over is that when writing programs people often make mistakes which prevent their programs from terminating. In popular jargon, programmers say 'My program went into an infinite loop!' It would clearly be beneficial if programmers could detect the existence of infinite loops in their programs before wasting computer resources in executing them. Hence the problem one would like to solve is that of determining whether an arbitrary program contains an infinite loop. Putting this another way, the problem is to determine whether an arbitrary program halts or not. This is called the halting problem. Its solution is an algorithm which, given an arbitrary program P and its input data D, can tell us whether or not P would eventually halt when executed with input data D.

Now the 'solution' to the halting problem used by mostcomputer installations is to time each program whilst it is being executed,and toforcibly abort the program if it uses more time than was allocatedto it.However, this is an undesirable solution for two reasons. Firstly,non-terminatingprograms will waste the entire time allocated to them. Secondly,it may happenwith certain programs that the programmer cannot calculatethe time required,and therefore a program may be aborted a short time beforeit would otherwisesuccessfully halt.

Thus one might expect that computer installations around the world are investing considerable effort in attempts to devise an algorithm which solves the halting problem. If they are, they are wasting their time, because no such algorithm exists. The halting problem is non-computable.This can be proved as follows.

                                                                               
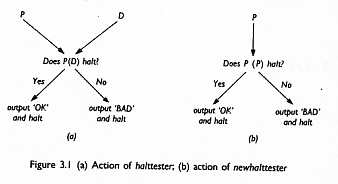
Let us assume for the moment that there is an algorithm for solving the halting problem. Call this algorithm halttester. As mentioned above, the algorithm has two inputs P and D, so that halttester(P, D) prints the answer 'OK' if program P would terminate when executed with input data D, and it prints'BAD' otherwise. The action of halttester is illustrated in Figure 3.1(a).

Since halttester tests the termination of a program P for any data D we can use it to construct a more limited algorithm which tests the termination of P when the data is P itself. The reader may find it strange that a program can be used as data in this way, but the situation is notunusual. A program is a representation of an algorithm and simply consistsof a sequence of characters (such as letters and digits). Any sequence ofcharacters can be input to a computer program. Whether the program does anythingsensible with the input is a separate issue. Actually there are many programsof practical interest whose input is a sequence of characters representinganother program: examples are compilers and editors (see Chapter 5).

Let us give the name newhalttester to this limited version of haIttester. Newhalttester can be written

module newhalttester(P)
(Checks whether program P halts if executed with data P)
       halttester(P, P)       (3.1)

The action of newhalttester is illustrated in Figure 3.1(b). If we assume that an algorithm haIttester exists, and that therefore newhalttester exists, we may construct the following algorithm, called funny, which has just one input P.

module funny(P)
(In order to write this module we are assuming that halttester exists)
       if newhalttester(P) outputs 'BAD'
               then halt
               else loop for ever (3.2).

                                                                          
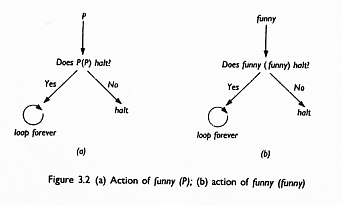
The action of algorithm funny is illustrated in Figure 3.2(a).

Finally, we consider what happens during execution of funny(funny) -that is, during execution of funny with its own program text as the input P. (This is quite legitimate, since P can be any sequence of characters.) The execution of funny(funny) is illustrated in Figure 3.2(b), which is the same as Figure 3.2(a) but with funny substituted for the input P. Figure3.2(b) clearly demonstrates a contradiction, since it shows on the one handthatif funny(funny) halts then it loops for ever, but on the other handthat iffunny(funny) loops forever then it halts. In other words the executionoffunny(funny) can neither halt nor loop forever.

The contradiction can be resolved only by admitting that the algorithm funny cannot exist. However, the only assumption made in deriving funny was that halttester exists. Hence if funny cannot exist then neither can halttester. We have therefore shown that no algorithm halttester forsolving the halting problem can exist, and hence that the halting problemis non-computable.

The proof above can be summarized as follows:

1. Assume we can write a program halttester.

2. Use it to construct another program funny (via an intermediate program newhalttester).

3. Show that funny has some impossible property (it can neither halt nor loop for ever).

4. Conclude that the assumption in step 1 must be wrong.

We have shown that there is no algorithm which can solve the halting problem. What does this mean? Surely there are some programswhich are so simple that it is obvious whether or not they halt. Of coursethere are -but there are lots of others where it is by no means so obvious.Consider, for example, an algorithm for testing the truth of Fermat's lasttheorem.This theorem states that there are no positive integers a, b, andc such thata" + b" = c" where n > 2.At present no proof or disproof ofthis theorem is known, though Fermat didclaim to have a proof.